Monthly Question...Are All Orbits Elliptical?
Well, no ... but the vast majority are at least slightly elliptical. This explains why a planet, for example, does not move with constant velocity along its entire orbit.
A circular orbit is referred to as a Copernican Orbit, based on the fact that despite his advanced thinking for the time, Copernicus was still wedded to the idea of a perfection in the universe that required all orbits to be perfectly circular. By definition then, all planets would have to move at a constant rate of speed along each of their orbital paths. Only a very few objects beyond our Solar System have been found to describe circular orbits.
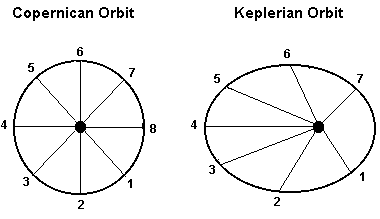
Copernicus' theory failed to accurately predict the positions of planets as viewed in the sky, so Johannes Kepler grappled with the problem of how the planets were actually seen to move. His first law of planetary motion postulated that the planets travel in elliptical orbits. His second law went on to state that as a planet draws nearer to the sun, its velocity increases. To be specific, he said that a line joining a planet to the sun sweeps out equal areas in equal units of time. In the Keplerian illustration above with the sun at the focus, the wedge from 1 to 2 encompasses the same area as the long, thin wedge from 3 to 4. The time unit from 1 to 2 is the same as from 3 to 4, but the length of the arc is shorter from 3 to 4. Therefore, a planet traveling from 3 to 4 does so at a more leisurely pace. (Note that the illustration is greatly exaggerated for our solar system, where the orbits are not nearly so elliptical.) The proof of the pudding was that Kepler's theory more accurately predicted the movements of the planets. However, in Kepler's time, no one yet knew why the planets assumed an elliptical orbit. That would be worked out about 75 years later with Newton's law of gravitation.





